Résoudre un Rubik's pocket cube avec Neo4j
17 mars 2017 · 5 min de lecture
Un pocket cube peut avoir 3 674 160 positions différentes. Pour une base de données NoSQL, ce nombre n’est même pas impressionnant.
Neo4j est une base de données de graphe NoSQL. Dans cet outil on pourrait modéliser les cubes, et les relier entre eux via les mouvements.
Et comme ce logiciel est capable de trouver le plus court chemin entre deux noeuds, pourrait-il nous donner la solution pour résoudre le cube en un minimum de coups d’après une position donnée ?
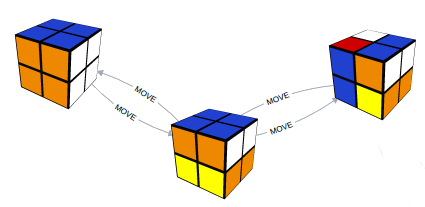
La réponse est oui, et en quelques millisecondes.
Voici comment procéder.
Représentation du cube
Tout d’abord, il faut écrire le code pour pouvoir manipuler un cube. Voici une façon de le représenter :
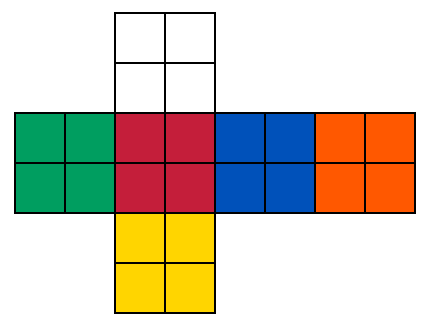
En programmation cela donne :
// b=blue T=top
// w=white F=front
// o=orange D=down
// r=red B=back
// y=yellow L=left
// g=green R=right
//
// --- ----- ---
// |w|w| |0 |1 | | T |
// |w|w| |2 |3 | | |
// --- --- --- --- ----------------------- ---------------
//|g|g|r|r|b|b|o|o| |4 |5 |6 |7 |8 |9 |10|11| | L | F | R | B |
//|g|g|r|r|b|b|o|o| |12|13|14|15|16|17|18|19| | | | | |
// --- --- --- --- ----------------------- ---------------
// |y|y| |20|21| | D |
// |y|y| |22|23| | |
// --- ----- ---
La position d’un cube est décrite par un tableau de 24 éléments :
// Le cube résolu peut se noter ainsi :
$position = array(
'w','w','w','w',
'g','g','r','r',
'b','b','o','o',
'g','g','r','r',
'b','b','o','o',
'y','y','y','y'
);
// ou, si on numérote les couleurs au lieu de les nommer :
$position = array(
0,0,0,0,
2,2,4,4,
3,3,5,5,
2,2,4,4,
3,3,5,5,
1,1,1,1
);
Toutefois, cette représentation a un inconvénient : imaginez un pocket cube résolu face à vous. Sa position vaut 000044335522443355221111. Tournez-le d’un quart de tour dans l’espace et vous obtiendrez par exemple 000033552244335522441111. Hors, il s’agit du même cube ! On peut touner 4 fois le cube dans un sens, sur les 6 faces et on obtient 24 notations qui désignent pourtant le même cube…
Pour réduire ce nombre à un, je trie les 24 positions par ordre numérique : 000022443355224433551111 | 000033552244335522441111 | 000044335522443355221111.... Le premier élément est utilisé comme identifiant (ID).
L’identifiant du cube résolu est : 000022443355224433551111.
On doit ensuite coder, entre autres, les méthodes suivantes :
- domove : pour jouer un coup, c’est-à-dire l’un des mouvements suivants :
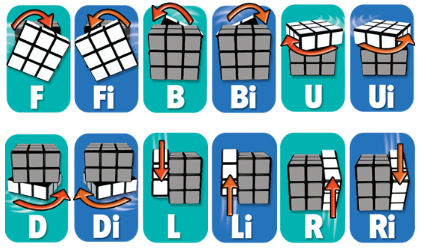Les lettres signifient : Front, Back, Up, Down, Left, Right dans le sens des aiguilles d’une montre, et “i” pour le sens inverse. Dans le programme, cela consiste simplement à échanger les éléments du tableau. Par exemple, un mouvement U (Up), va faire tourner les éléments 0 à 3 et décaler les éléments 4 à 11 (cf. la représentation du cube en haut de page). - undomove : pour annuler un mouvement.
- setpos : pour définir une position, telle que saisie par un utilisateur.
- rotx : Jouer U, Di, et votre pocket cube a fait 1/4 de tour.
- roty : Jouer Li, R.
Génération de toutes les positions
Ou comment générer les 3 674 160 identifiants décrivant tous les états possibles d’un pocket cube, ainsi que les liens entre eux.
Voici l’algorithme :
on part du cube résolu
on note que sa position est à étudier
tant qu'il reste des position à étudier :
récupérer l'ID (A) du cube
ajouter l'ID (A) dans le fichier des NOEUDS si ce n'est déjà fait
pour chacun des 12 coups possibles :
jouer le coup
ajouter l'ID (B) de la position obtenue dans le fichier des NOEUDS si ce n'est déjà fait
marquer que la position (B) est à étudier si ce n'est déjà fait
ajouter le lien A->B dans le fichier des RELATIONS
défaire le coup
marquer la position ID (A) comme faite.
Voilà le travail en cours :
Après plusieurs heures, j’obtiens deux beaux fichiers CSV de 110 et 585 Mo :
nodes.csv pour les noeuds :
pos:ID;:LABEL
000022443355224433551111;Cube
004441330522413305225511;Cube
004441330522330522415151;Cube
000244351522343052411351;Cube
000533512244312501344215;Cube
000533512244343125011452;Cube
000433502524343522411151;Cube
002234051524305312413451;Cube
021425330515430423125014;Cube
edges.csv pour les relations entre eux :
:START_ID;:END_ID;:TYPE
000022443355224433551111;004441330522413305225511;MOVE
000244351522343052411351;004441330522330522415151;MOVE
000533512244312501344215;000533512244343125011452;MOVE
000433502524343522411151;002234051524305312413451;MOVE
004550212433143501341225;021425330515430423125014;MOVE
000233551524341423112054;001232540524305123113454;MOVE
021425330405130211235544;031225351045130414235240;MOVE
002341441432535535011022;024552131053404523412130;MOVE
001142542432013435355120;002341441432015355352120;MOVE
Vous aurez remarqué que j’ai prévu l’entête pour l’import dans Neo4j.
Import des données dans Neo4j
On supprime la base existante :
sudo rm -rf /data/databases/*
On se place dans le dossier où se trouvent nos fichiers CSV :
cd /var/lib/neo4j/import/data
Import des CSV dans Neo4j :
/var/lib/neo4j/bin/neo4j-admin import \
--into /data/databases/graph.db \
--nodes nodes.csv \
--relationships edges.csv \
--delimiter ";" \
--array-delimiter "-" \
--quote "'"
Résultat des opérations :
IMPORT DONE in 1m 8s 438ms.
Imported:
3674160 nodes
10631005 relationships
3674160 properties
Peak memory usage: 79.57 MB
NB : il faut ensuite redémarrer Neo4j : sudo service neo4j restart.
Résoudre le cube
Cela consiste à trouver le plus court chemin entre deux noeuds. A l’aide d’une interface graphique on fait saisir les 6 faces du cube à un utilisateur. On génère l’identifiant de sa position, par exemple 002140534352524214031513. On requête Neo4j, en cherchant le chemin le plus court jusqu’au cube résolu dont l’identifiant est 000022443355224433551111 :
MATCH (c1:Cube), (c2:Cube), p = shortestPath((c1)-[m:MOVE*]-(c2))
WHERE c1.pos="002140534352524214031513" AND c2.pos="000022443355224433551111"
RETURN p
On obtient en 0.08 secondes :
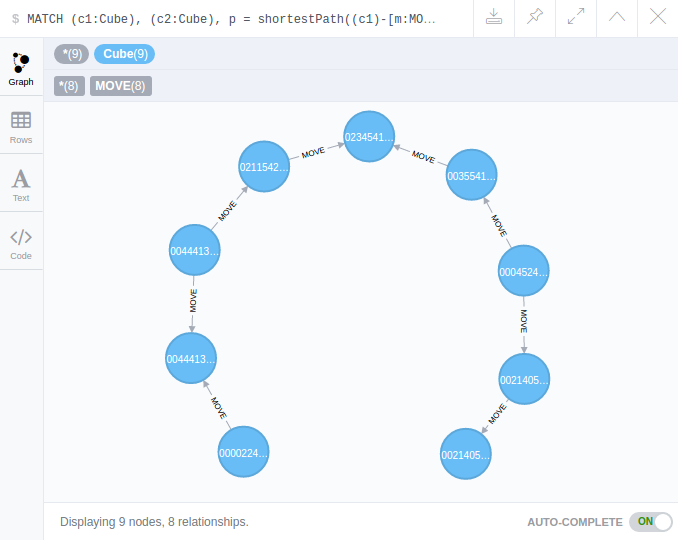
Remarque : Un lien non dirigé suffirait entre deux cubes, car on veut matérialiser le passage de l’un à l’autre via un mouvement. La direction n’a ici aucune importance car il y a réciprocité. Dans Neo4j il n’y a que des liens dirigés.
Il n’est pas possible d’associer le nom du coup au lien [MOVE] car on a simplifié 24 notations de positions en 1.
Par conséquent, pour trouver le nom du coup à jouer entre deux noeuds (F, B, D, Di, L…), on procède de la façon suivante : On part de la position donnée, on joue les 12 coups possibles, et on regarde si l’identifiant de la nouvelle position correspond à celui du noeud suivant.
J’ai automatisé des séries de tests. Le cube est résolu au plus en 14 coups !
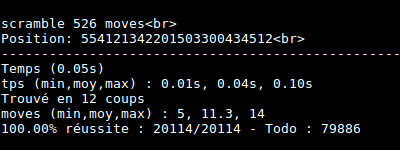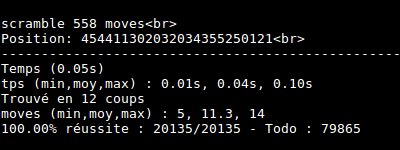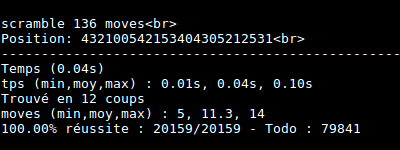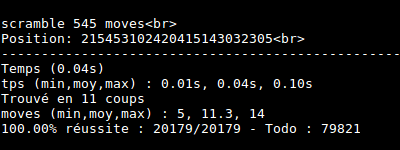
Conclusion
Vous trouverez sur Google Play un solveur de pocket cube.
Have fun.