Comment programmer un jeu d'échecs ?
22 septembre 2014 · 11 min de lecture
Vous souhaitez relever le défi d’écrire un jeu d’échecs ? Ou simplement comprendre comment un ordinateur peut jouer correctement ? Je vous propose d’étudier le code source du programme écrit pour l’occasion :
“Jepychess” qui signifie à peu de chose près “JeffProd Simple Python Chess Program”.
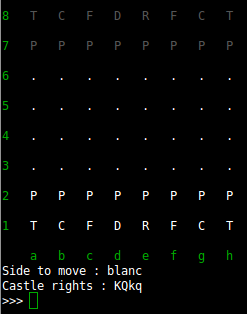
Dans un but de simplicité, cet article se concentre uniquement sur le moteur du jeu, non sur une interface graphique.
Le projet JePyChess est hébergé sur GitHub. Les lignes de code peuvent être améliorées. N’hésitez pas à signaler des erreurs ou suggérer des modifications, sachant que l’objectif n’est pas d’en faire une bête de course.
Quel langage de programmation choisir ?
On peut écrire un jeu d’échecs dans tous les langages. Tout dépend de votre objectif et des appareils pour lesquels il est destiné (smartphone, tablette, ordinateur…).
Vous avez à votre disposition de nombreux langages de programmation :
PHP, Java, Javascript, Ruby, Python, C, C++, C#, Perl…
Si vous souhaitez confronter votre programme à Deep Blue, choisissez un langage de bas niveau ou compilé, comme le C, voire même l’assembleur ! Car demander à un ordinateur de jouer aux échecs, c’est lui demander de nombreux calculs. Il faut donc être très rapide pour être au top.
Je vous propose un code source en Python pour les raisons suivantes :
- ce langage ne nécessite pas de compilation. On peut écrire le code dans un éditeur de texte et l’exécuter instantanément;
- il est disponible sur toutes les plateformes (Windows, Mac, Linux);
- vous pourrez implémenter une interface graphique ultérieurement dans le même langage;
- on pourra jouer en ligne de commande;
- c’est un langage accessible aux débutants;
Pour installer Python sur votre ordinateur, rendez-vous sur le site officiel et téléchargez la dernière version.
Maintenant entrons dans le vif du sujet.
Composition d’un jeu d’échecs
On peut décomposer un logiciel d’échecs aux éléments suivants :
- un échiquier;
- des pièces d’échecs;
- un moteur de jeu;
- une interface graphique.
Ainsi, le projet que je vous présente est composé actuellement des fichiers :
- main.py : le programme principal qui affiche l’échiquier en mode console et répond aux sollicitations de l’utilisateur;
- engine.py : le moteur du jeu, capable d’analyser une position de l’échiquier et déterminer le meilleur coup;
- board.py : comprend les attributs et les méthodes de l’objet ‘échiquier’;
- piece.py : comprend les attributs et les méthodes des pièces d’échecs.
J’ouvre donc une petite parenthèse pour vous exposer brièvement la programmation orientée objet.
Pour schématiser, ce type de programmation s’efforce de considérer tout élément comme un objet encapsulé dans une boite noire. Cet objet a des caractéristiques ou attributs (ex : couleur, dimension) et des méthodes (par exemple pour une voiture : démarrer, arrêter, accélérer). Ceci permet de bien isoler les variables et regrouper les actions effectuées par chaque objet.
L’échiquier
Il existe plusieurs façons de représenter l’échiquier. Etant composé de 64 cases, le plus simple en programmation est d’utiliser un tableau de 64 éléments. Les index de ce tableau seront numérotés de 0 à 63. Ainsi la case a8 correspond à 0, et h1 à 63.
coord=[
'a8','b8','c8','d8','e8','f8','g8','h8',
'a7','b7','c7','d7','e7','f7','g7','h7',
'a6','b6','c6','d6','e6','f6','g6','h6',
'a5','b5','c5','d5','e5','f5','g5','h5',
'a4','b4','c4','d4','e4','f4','g4','h4',
'a3','b3','c3','d3','e3','f3','g3','h3',
'a2','b2','c2','d2','e2','f2','g2','h2',
'a1','b1','c1','d1','e1','f1','g1','h1',
]
Avec la définition du tableau ci dessus, coord[3] retournera ‘d8’.
Sur les cases de l’échiquier on peut mettre une pièce… ou pas.
Donc pour des raisons pratiques, on mettra toujours un objet-pièce sur chaque case de l’échiquier mais cet objet pourra être vide :
self.cases = [
Piece('TOUR','noir'),Piece('CAVALIER','noir'),Piece('FOU','noir'),Piece('DAME','noir'),Piece('ROI','noir'),Piece('FOU','noir'),Piece('CAVALIER','noir'),Piece('TOUR','noir'),
Piece('PION','noir'),Piece('PION','noir'),Piece('PION','noir'),Piece('PION','noir'),Piece('PION','noir'),Piece('PION','noir'),Piece('PION','noir'),Piece('PION','noir'),
Piece(),Piece(),Piece(),Piece(),Piece(),Piece(),Piece(),Piece(),
Piece(),Piece(),Piece(),Piece(),Piece(),Piece(),Piece(),Piece(),
Piece(),Piece(),Piece(),Piece(),Piece(),Piece(),Piece(),Piece(),
Piece(),Piece(),Piece(),Piece(),Piece(),Piece(),Piece(),Piece(),
Piece('PION','blanc'),Piece('PION','blanc'),Piece('PION','blanc'),Piece('PION','blanc'),Piece('PION','blanc'),Piece('PION','blanc'),Piece('PION','blanc'),Piece('PION','blanc'),
Piece('TOUR','blanc'),Piece('CAVALIER','blanc'),Piece('FOU','blanc'),Piece('DAME','blanc'),Piece('ROI','blanc'),Piece('FOU','blanc'),Piece('CAVALIER','blanc'),Piece('TOUR','blanc')
]
Ainsi, en parcourant les index (de 0 à 63) du tableau ci-dessus :
- self.cases[1] est un cavalier noir;
- self.cases[35] est vide;
- self.cases[60] est le roi blanc.
Pour nous aider j’ai créé l’image ci-dessous :
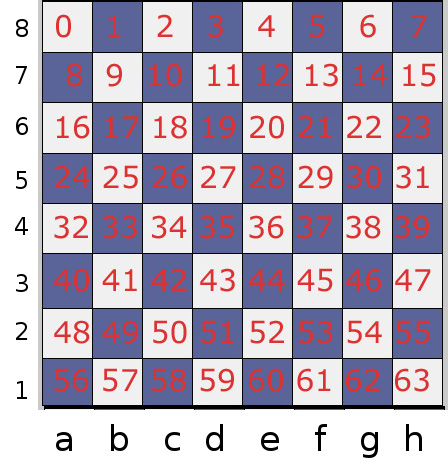
Outre ses cases, l’échiquier possède les attributs suivants :
- le camp qui a le trait (aux noirs ou blancs de jouer);
- la case d’une prise en passant;
- le nombre de coups joués depuis le début de la partie;
- un historique des coups joués;
- les droits au roque.
On va créer dans cet objet ‘Echiquier’ les méthodes suivantes :
- générer la liste de tous les coups pour un camp donné;
- possibilité de définir une position des pièces au format FEN;
- possibilité d’exporter cette position avec la notation FEN;
- déplacer une pièce selon les règles du jeu;
- annuler le dernier coup joué;
- changer le joueur qui a le trait;
- savoir si un roi est en échec;
- savoir si une pièce est attaquée;
- afficher l’échiquier en mode console;
- afficher l’historique des coups joués;
- donner une note à une position.
Les pièces
Comme vous le savez les pièces sont : roi, dame, tour, cavalier, fou, pion. Certaines sont plus importantes que d’autres. On peut donc leur attribuer une valeur, par exemple 9 points pour la dame, 5 pour la tour, etc. Comme le roi ne peut pas être pris, il n’est pas utile de lui donner une valeur.
nomPiece=(VIDE,'ROI','DAME','TOUR','CAVALIER','FOU','PION')
valeurPiece=(0,0,9,5,3,3,1)
Avec le code ci-dessus, une case vide et le roi ont 0 point, la dame 9, la tour 5, cavalier et fou 3 et enfin le pion : 1 point.
Une pièce a les attributs suivants :
- un nom (roi, dame, tour…);
- une couleur (blanc, noir);
- une valeur (définie en points ci-dessus).
On peut les déplacer d’une case à une autre selon les règles propres à chacune. On va donc créer les fonctions permettant de trouver les cases de destination d’une pièce d’après sa case de départ.
Déplacement des pièces
Prenons un cas concret :
On a une tour en case a4 (index 32) (voir image plus haut des cases numérotées).
On va la déplacer d’une case à gauche. Elle se retrouve donc en case 32-1=31 soit h5 ! impossible !
Nous utiliserons donc la méthode de Robert Hyatt appelée ‘mailbox’ qui permet d’éviter ce débordement. Il s’agit de deux tableaux de 64 et 120 éléments, ressemblant à une boite à lettres selon son créateur, d’où son nom :
tab120 = (
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, 0, 1, 2, 3, 4, 5, 6, 7, -1,
-1, 8, 9, 10, 11, 12, 13, 14, 15, -1,
-1, 16, 17, 18, 19, 20, 21, 22, 23, -1,
-1, 24, 25, 26, 27, 28, 29, 30, 31, -1,
-1, 32, 33, 34, 35, 36, 37, 38, 39, -1,
-1, 40, 41, 42, 43, 44, 45, 46, 47, -1,
-1, 48, 49, 50, 51, 52, 53, 54, 55, -1,
-1, 56, 57, 58, 59, 60, 61, 62, 63, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1
)
tab64 = (
21, 22, 23, 24, 25, 26, 27, 28,
31, 32, 33, 34, 35, 36, 37, 38,
41, 42, 43, 44, 45, 46, 47, 48,
51, 52, 53, 54, 55, 56, 57, 58,
61, 62, 63, 64, 65, 66, 67, 68,
71, 72, 73, 74, 75, 76, 77, 78,
81, 82, 83, 84, 85, 86, 87, 88,
91, 92, 93, 94, 95, 96, 97, 98
)
Avec notre tour en a4 : dans le tableau ’tab64’ à l’index 32, nous obtenons la valeur 61.
On la déplace d’une case à gauche, on obtient 60.
Regardons le 60ème élément dans le tableau ’tab120’ : cela donne -1.
Il s’agit de la valeur définie pour indiquer une sortie de plateau.
Toujours d’après ce tableau ’tab64’ on peut définir les ‘vecteurs’ suivants pour les déplacements des pièces :
deplacements_tour=(-10,10,-1,1)
deplacements_fou=(-11,-9,11,9)
deplacements_cavalier=(-12,-21,-19,-8,12,21,19,8)
Et cerise sur le gâteau ça suffit ! inutile de spécifier des vecteurs pour la dame et le roi car ceux-ci se déplacent à la fois comme le fou et la tour, mais d’une seule case à la fois pour le roi.
Intelligence artificielle : Le moteur de jeu
Nous entrons dans le coeur du sujet.
Inutile de réinventer la roue, des mathématiciens ont imaginé des algorithmes de recherche du meilleur coup à jouer. Le plus approprié pour les échecs est l’algorithme alpha-béta.
Concrètement, cet technique permet de créer un arbre de positions de l’échiquier en attribuant pour chacune une note d’évaluation.
L’évaluation
Chaque position de l’échiquier est analysée selon plusieurs critères. Une note est calculée en fonction des pièces présentes et de nombreux bonus/malus. Il s’agit de ’l’évaluation’.
Voici la plus simple des fonctions d’évaluation ne prenant en compte que le matériel présent :
def evaluer(self):
'''A wonderful evaluate() function
returning actually only the material score'''
WhiteScore=0
BlackScore=0
# Parsing the board squares from 0 to 63
for pos1,piece in enumerate(self.cases):
# Material score
if(piece.couleur=='blanc'):
WhiteScore+=piece.valeur
else:
# NB : here is for black piece or empty square
BlackScore+=piece.valeur
if(self.side2move=='blanc'):
return WhiteScore-BlackScore
else:
return BlackScore-WhiteScore
On pourrait compléter cette fonction d’évaluation avec les bonus et malus suivants (et en plus, le malus des uns fait le bonus des autres) :
- pion passé : pion qui ne rencontrera plus de pion adverse et qui peut donc aller en promotion;
- tour en 7ème rangée;
- roi dans une colonne ouverte;
- pions du roque avancés;
- le roi a été déplacé et ne peut plus roquer;
- pions doublés (2 pions dans la même colonne);
- pion isolé : pion qui ne peut plus être protégé par un autre pion.
On peut également accorder des bonus/malus selon l’avancement de la partie :
- en début de partie, il est préférable de roquer pour protéger le roi. Au contraire, en fin de partie, il faut placer le roi au centre pour éviter un mat sur une arrête ou dans un coin de l’échiquier;
- un cavalier peut atteindre un plus grand nombre de cases s’il est au centre;
- les pions prennent de la valeur s’ils approchent la 8ème rangée.
La recherche du meilleur coup
C’est à l’ordinateur de jouer. Il génère la liste de tous les coups possibles. Il déplace une pièce. Il attribue une note à la position. Il se mets à la place de l’adversaire et il fait exactement la même chose, et ainsi de suite. Il faut donc préciser au moteur de recherche une profondeur fixe (par exemple 5 déplacements) ou un temps donné de réflexion. Le programme va donc élaborer un arbre de recherche. Il construit une arborescence de positions de l’échiquier où chacune est notée.
Il est impossible d’explorer toutes les branches comme on pourrait le faire dans un jeu de morpions ou de puissance 4. L’algorithme alpha-béta permet un élagage des branches.
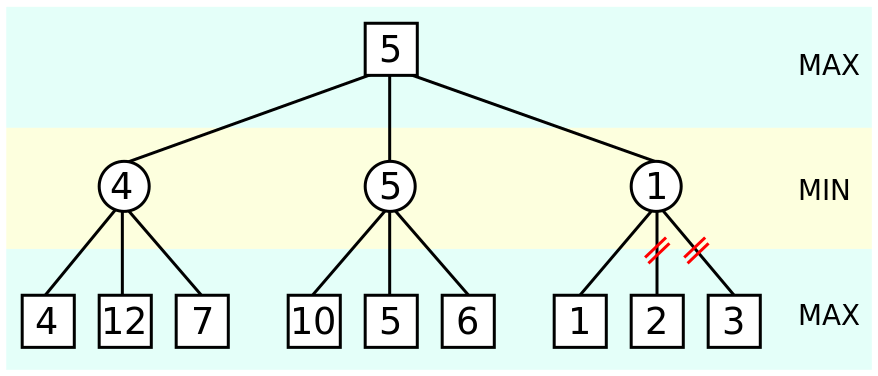
“Poda alfa-beta”. Sous licence CC BY-SA 3.0 via Wikimedia Commons.
Le meilleur coup est enregistré dans un tableau nommé ‘Triangular PV-Table’ (Principal Variation). Il s’agit d’un tableau d’éléments indexés par le numéro de profondeur en rapport au début de la recherche. Il a pour but de collecter la meilleure ligne de coups successifs. Les éléments sont les meilleurs coups trouvés et enregistrés dans alpha-beta. Il est donc recommandé de suivre cette ligne de coups afin de permettre un élagage efficace, puis les coups avec prise.
Voici l’algorithme alphabéta de JePyChess :
def alphabeta(self,depth,alpha,beta,b):
# We arrived at the end of the search : return the board score
if(depth==0):
return b.evaluer()
# TOTO : return quiesce(alpha,beta)
self.nodes+=1
self.pv_length[b.ply] = b.ply
# Do not go too deep
if(b.ply >= self.MAX_PLY-1):
return b.evaluer()
# Extensions
# If king is in check, let's go deeper
chk=b.in_check(b.side2move) # 'chk' used at the end of func too
if(chk):
depth+=1
# Generate all moves for the side to move. Those who
# let king in check will be processed in domove()
mList=b.gen_moves_list()
f=False # flag to know if at least one move will be done
for i,m in enumerate(mList):
# Do the move 'm'.
# If it lets king in check, undo it and ignore it
# remind : a move is defined with (pos1,pos2,promote)
# i.e. : 'e7e8q' is (12,4,'q')
if(not b.domove(m[0],m[1],m[2])):
continue
f=True # a move has passed
score=-self.alphabeta(depth-1,-beta,-alpha,b)
# Unmake move
b.undomove()
if(score>alpha):
# this move caused a cutoff,
if(score>=beta):
return beta
alpha = score
# Updating the triangular PV-Table
self.pv[b.ply][b.ply] = m
j = b.ply + 1
while(j<self.pv_length[b.ply+1]):
self.pv[b.ply][j] = self.pv[b.ply+1][j]
self.pv_length[b.ply] = self.pv_length[b.ply + 1]
j+=1
# If no move has been done : it is DRAW or MAT
if(not f):
if(chk):
return -self.INFINITY + b.ply # MAT
else:
return 0 # DRAW
return alpha
Améliorations possibles
Le code a été écrit “au plus simple”, le programme n’est donc pas de niveau international, mais essayez quand même de le battre !
Il est possible par exemple de l’optimiser pour augmenter la vitesse de calcul.
Il reste également à implémenter :
- move ordering : suivre la variation principale et les captures de pièces en premier pour la recherche des meilleurs coups;
- la règle des 50 coups sans prise (partie nulle);
- la règle des 3 répétitions de position (partie nulle);
- la gestion du temps (partie en blitz, recherche par temps fixe…);
- détecter les parties nulles pour matériel insuffisant;
- bibliothèque d’ouvertures;
- base de données de fins de partie;
- recherche “quiescent” : au lieu de stopper net sur la note d’une position, si une pièce vient d’être prise, il peut s’avérer utile de continuer la recherche des prises uniquement, ceci afin de limiter l’effet d’horizon.
Sachez également que ces techniques ne sont qu’une infime partie de toutes celles qui existent dans le monde passionnant et expérimental de la programmation des jeux d’échecs.
Liens externes
Vous trouverez sur internet de nombreuses ressources. Il existe même des tournois entre programmes d’échecs, et des classements par ELO. Voici quelques liens :
Code source de JePyChess sur GitHub : jeu d’échecs en ligne de commande écrit en Python.
Code source d’un programme d’échecs écrit en C, et qui m’a inspiré :
TSCP
Un site en anglais sur la programmation des jeux d’échecs :
Chess Programming Wiki